optimizing_cpp(7)
七、内存访问优化
1.缓存
优化访存主要就是优化cahce的访问,因此先系统复习下关于cache的相关知识。
现代cpu大多拥有三级缓存L1L2L3。
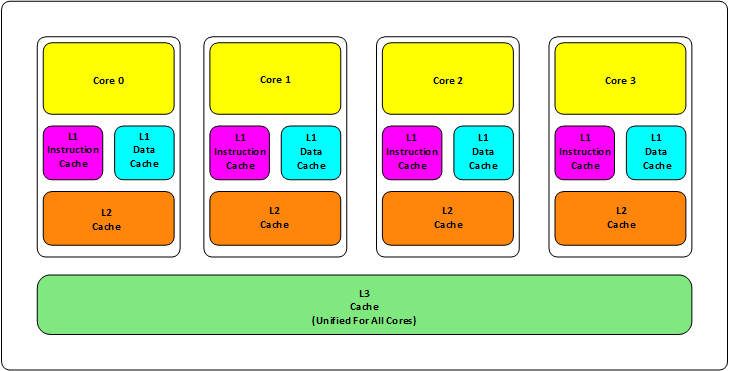
- L1缓存分成两种,一种是指令缓存,一种是数据缓存。L2缓存和L3缓存不分指令和数据。
- L1和L2缓存在每一个CPU核中,L3则是所有CPU核心共享的内存。
- L1、L2、L3的越离CPU近就越小,速度也越快,越离CPU远,速度也越慢。
三级缓存和RAM读取速度的对比:
- L1 的存取速度:4 个CPU时钟周期
- L2 的存取速度: 11 个CPU时钟周期
- L3 的存取速度:39 个CPU时钟周期
- RAM内存的存取速度:107 个CPU时钟周期
cache与RAM的映射方式:
直接映射:一个cache块对应多个内存块,一个内存块只能对应一个cache块
全相联映射:任何一个内存块都能对应任何一个cache块,但是比较块号所需时间长
组相联映射:将前两者结合起来,cache分为多个每个组内有多个块,内存也分块,每一块对应一cahce组,可以占用组内的任意cache块
离cpu最近的可以直接相联,较近的可以组相联,最远的可以全相联,距离越远对cache速度的要求就越低对利用率的强调就越高。
cache的最小存储单位:cache line即上面所说的块,一般大小为64byte(512位)
在组相联映射中(N-wayassociative cache fill)将N个cache line绑成一组,先找到相关的组,再在这个组中找到相关的cacheline
我们举个栗子:
Intel 大多数处理器的L1 Cache都是32KB,8-Way 组相联,Cache Line 是64 Bytes。这意味着,
- 32KB的可以分成,32KB / 64 = 512 条 Cache Line。
- 因为有8 Way,于是会每一Way 有 512 / 8 = 64 条 Cache Line。
- 于是每一way就有 64 x 64 = 4096 Bytes 的内存。
为了方便索引内存地址,
- Tag:每条 Cache Line 前都会有一个独立分配的 24 bits来存的 tag,其就是内存地址的前24bits
- Index:内存地址后续的6个bits则是在这一Way的是Cache Line 索引,2^6 = 64 刚好可以索引64条Cache Line
- Offset:再往后的6bits用于表示在Cache Line 里的偏移量
如下图所示:(图片来自《Cache: a place for concealment and safekeeping》)
当拿到一个内存地址的时候,先拿出中间的 6bits 来,找到是哪组。
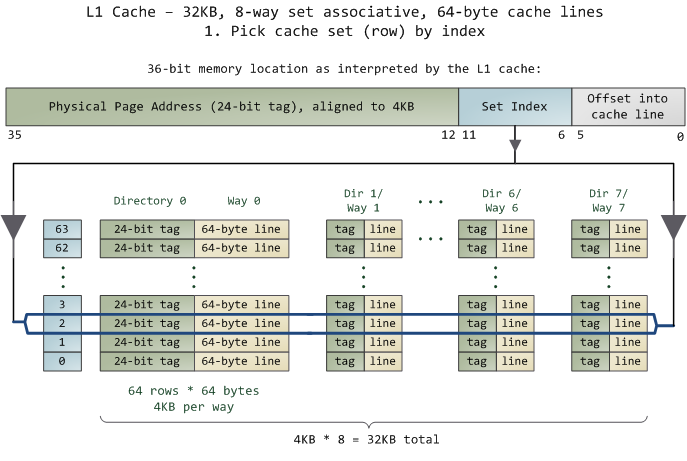
然后,在这一个 8 组的 cache line 中,再进行 O(n) n=8 的遍历,主是要匹配前 24bits 的 tag。如果匹配中了,就算命中,如果没有匹配到,那就是 cache miss,如果是读操作,就需要进向后面的缓存进行访问了。L2/L3 同样是这样的算法。而淘汰算法有两种,一种是随机一种是 LRU。现在一般都是以 LRU 的算法(通过增加一个访问计数器来实现)
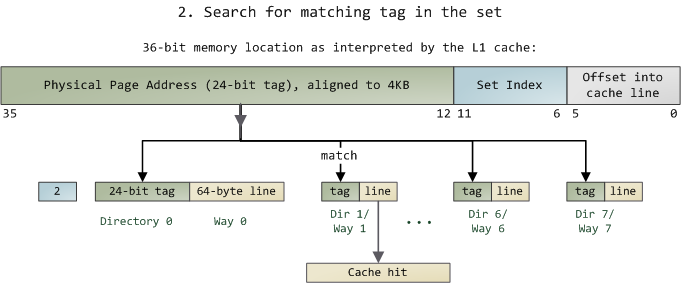
这也意味着:
- L1 Cache 可映射 36bits 的内存地址,一共 2^36 = 64GB的内存
- 当CPU要访问一个内存的时候,通过这个内存中间的6bits 定位是哪个set,通过前 24bits 定位相应的Cache Line。
- 就像一个hash Table的数据结构一样,先是O(1)的索引,然后进入冲突搜索。
- 因为中间的 6bits 决定了一个同一个set,所以,对于一段连续的内存来说,每隔4096的内存会被放在同一个组内,导致缓存冲突(解释一下,随着地址的增加,后12位数字会不断循环,间隔就是2的12次方4096,所以每隔4096的地址就会缓存冲突)
此外,当有数据没有命中缓存的时候,CPU就会以最小为Cache Line的单元向内存更新数据。当然,CPU并不一定只是更新64Bytes,因为访问主存实在是太慢了,所以,一般都会多更新一些。好的CPU会有一些预测的技术,如果找到一种pattern的话,就会预先加载更多的内存,包括指令也可以预加载。这叫 Prefetching 技术 (参看,Wikipedia 的 Cache Prefetching 和 纽约州立大学的 Memory Prefetching)。比如,你在for-loop访问一个连续的数组,你的步长是一个固定的数,内存就可以做到prefetching。
缓存的一致性问题
cache的写策略:
- write back(写回)写到cache,等需要时再flush到内存中
- write throuth(写直达)直接写道内存和cache中
为了提高写的性能,一般采用write back
缓存一致性协议:
- 监听cache一致性协议:当多个核共享总线时,总线上传递的信号都能被连接到总线的所有核“看”到。当某个核更新它cache中x的副本时,它将更新消息在总线上广播,若核1在监听总线,它就会知道x已经更新并且将自己cache中x的副本标记为非法的。实际情况是广播会通知其它核包含x的整个Cache行已经更新。
- 基于目录的cache一致性协议:使用一个叫目录的数据结构来存储每个内存行的状态。一般的,这个数据结构是分布式的。当一个高速缓存行被读入时,如核0的cache,与这个高速缓存行相对应的目录项就会更新,表示核0有这个行的副本。当一个变量需要更新时,就会查询目录,并将所有包含该变量高速缓存行设置为非法。
与程序员相关的CPU缓存知识 | 酷 壳 - CoolShell酷壳的这篇文章还有示例,可以好好看一下,加深理解。
2.一起使用的函数应该放在一起
如果在代码内存中使用的函数彼此接近,那么代码缓存的工作效率最高。函数通常按照它们在源代码中出现的顺序存储。因此,最好将代码中最关键部分中使用的函数集中在同一个源文件中,这些函数彼此相邻。将经常使用的函数与很少使用的函数分开,并将很少使用的分支(如错误处理)放在函数的末尾或单独的函数中。
有时,为了模块化,函数被保存在不同的源文件中。例如,在一个源文件中有父类的成员函数,在另一个源文件中有派生类的成员函数,这样做可能比较方便。如果父类和派生类的成员函数是在程序的相同关键部分被调用的,那么在程序内存中保持这两个模块的连续是有利的。这可以通过控制模块链接的顺序来实现。链接顺序通常是模块在项目窗口或makefile中出现的顺序。你可以通过向链接器请求映射文件来检查内存中函数的顺序。映射文件告诉每个函数相对于程序开始的地址。映射文件包含从静态库链接(*.lib或.a* )的库函数的地址,但不是动态库(*.dll或.so*)。没有一种简单的方法可以控制动态链接库函数的地址。
3.一起使用的变量应该放在一起
如果cpu缓存没有命中,那么代价会非常高,所以经常一起使用的数据片段应该在内存中彼此靠近,以便cpu缓存能够同时命中。如果可能,避免全局变量和静态变量,并避免动态内存分配(new和delete)。
如果代码中有大数据结构,那么存储数据的顺序可能非常重要。例如,如果一个程序有两个数组,a 和 b,并且元素的访问顺序是a[0], b[0], a[1], b[1],…,然后,你可以通过将数据组织为结构体的数组来提高性能:
1 | // Example 9.1a |
如果按如下方法组织数据,那么这个例子中的数据可以在内存中被按顺序访问:
1 | // Example 9.1b |
使用例 9.1b中这样的数据结构,程序代码中将不会有额外的开销。相反的,代码将变的更加简单,因为只需要计算一个数组的地址,而不是两个。
一些编译器将为不同的数组使用不同的内存空间,即使它们从未同时被使用过。例如:
1 | // Example 9.2a |
在这里,可以为 a 和 b 使用相同的内存区域,因为它们的活动范围不重叠。通过将 a 和 b 放入 union 中,可以节省大量缓存空间:
1 | // Example 9.2b |
当然,使用 union 不是一种安全的编程实践,因为如果 a 和 b 的使用重叠,编译器不会发出警告。你应该只对占用大量缓存空间的大型对象使用此方法。将简单变量放入union中不是最佳选择,因为它会阻止寄存器变量的使用。
4.数据对齐
如果将变量存储在可被变量大小整除的内存地址中,则访问该变量的效率最高。例如,double 占用 8字节的存储空间。因此,最好将其存储在可被 8整除的地址中。大小应该总是 2的幂。大于 16字节的对象应该存储在可被 16整除的地址中。你通常可以假设编译器会自动处理这种对齐。
你可以选择按cache line大小对齐大型对象和数组(通常是 64字节)。这可以确保对象或数组的开头与cache line的开头一致。一些编译器会自动对齐大的静态数组,但你也可以通过以下方式显示指定:
1 | __declspec(align(64)) int BigArray[1024]; // Windows syntax |
或
1 | int BigArray[1024] __attribute__((aligned(64))); // Linux syntax |
5.动态分配内存
对象和数组可以通过 new 和 delete 或 malloc 和 free 动态分配。在编译时期不知道所需的内存大小时,这可能非常有用。下面是动态内存分配的四种典型用法:
- 可以在编译时不知道数组大小的情况下动态分配大数组。
- 当编译时不知道对象总数时,可以动态分配可变数量的对象。
- 可以动态分配文本字符串和类似大小可变对象。
- 对于栈来说太大的数组可以动态分配。
动态分配内存的优点有:
- 在某些情况下提供了更清晰的程序结构。
- 不会分配超过所需的空间。缓存效率与为了覆盖最坏的情况下最大可能的内存要求,固定大小的数组变的很大时相比,会高的多。
- 当不能预先给出所需内存空间的合理上限时,这是非常有用的。
动态分配内存的缺点有:
- 动态分配和释放内存的过程比其他类型的存储需要更多的时间。见7.1 不同类型变量的存储。
- 当以随机顺序分配和释放不同大小的对象时,堆空间就会变得碎片化。这使得数据缓存效率低下。
- 如果已分配的数组已满,则可能需要调整其大小。这可能需要分配一个新的更大的内存块,并将整个内容复制到新块中。指向旧块中的数据的任何指针都将失效。
- 当堆空间变得过于碎片化时,堆管理器将启动垃圾收集。此垃圾收集可能在不可预测的时间开始,并在用户等待响应的不方便的时间导致程序执行的延迟。
- 程序员有责任确保已分配的所有内容也被释放。如果不这样做,将导致堆被填满。这是一种常见的编程错误,称为内存泄漏。
- 序员有责任确保在释放对象之后没有对象被访问。没有这么做也是一个常见的编程错误。
- 所分配的内存可能不是最佳对齐的。有关如何对齐动态分配的内存,请参见12.8 对齐动态分配的内存。
- 编译器很难优化使用指针的代码,因为它不能排除别名(参见8.3 编译器优化的障碍:指针别名)。
- 当行长度在编译时是未知的,矩阵或多维数组的效率较低,因为在每次访问时需要额外的工作来计算行地址。编译器可能无法使用归纳变量对其进行优化。
在决定是否使用动态内存分配时,权衡利弊是很重要的。当数组的大小或对象的数量在编译时已知或可以知道合理的上限时,没有理由使用动态内存分配。
当分配的数量有限时,动态内存分配的成本可以忽略不计。因此,当一个程序有一个或几个可变大小的数组时,动态内存分配是有利的。另一种解决方案是将数组设置得非常大,以覆盖最坏的情况,但这会浪费缓存空间。如果一个程序有几个大数组,并且每个数组的大小是关键步长(参见9.2 缓存结构)的倍数,那么很可能会在数据缓存中引起竞争。
如果一个数组中的元素数量在程序执行期间增长,那么最好从一开始就分配最终的数组大小,而不是一步一步地分配更多的空间。在大多数系统中,你无法增加已经分配的内存块的大小。如果最终大小无法预测,或者预测结果太小,那么就需要分配一个新的更大内存块,并将旧内存块的内容复制到新的更大内存块的开头。当然,这是低效的,并且会导致堆空间变得碎片化。另一种方法是保留多个内存块,要么以链表的形式,要么以内存块的索引的形式。具有多个内存块的方法使得对单个数组元素的访问更加复杂和耗时。
一个可变数量的对象集合通常被实现为一个链表。链表中的每个元素都有自己的内存块和指向下一个块的指针。链表的效率不如线性数组,原因如下:
- 每个对象都是单独分配的。分配、释放和垃圾收集需要大量的时间。
- 对象没有连续地存储在内存中。这会降低数据缓存的效率。
- 额外的内存空间用于链接指针和堆管理器为每个分配的块存储的信息。
- 遍历链表比遍历线性数组要花费更多的时间。在加载前一个元素指针之前,不能加载任何指针。这就形成了一个关键的依赖链,这会妨碍乱序执行。
为所有对象分配一个大内存块(内存池)通常比为每个对象分配一个小内存块效率更高。
使用 new 和 delete 分配可变大小的数组的一个鲜为人知的替代方法是使用 alloca 分配来代替。这是一个在栈上而不是堆上分配内存的函数。内存空间在当从调用 alloca 的函数返回时会被自动释放。在使用 alloca 时,不需要显式地释放空间。与 new 和 delete 或 malloc 和 free 相比,alloca 的优势有:
- 分配过程的开销很小,因为微处理器有硬件支持对栈的操作。
- 由于堆栈的先入后出特性,内存空间不会变得支离破碎。
- 重新分配没有成本,因为它在函数返回时将自动执行。不需要垃圾收集。
- 所分配的内存与栈上的其他对象是连续的,这使得数据缓存非常高效。
下面的例子将展示如何适应alloca分配可变大小的数组:
1 |
|
显然,函数不应该返回任何使用 alloca 分配的指针或引用,因为它在函数返回时被释放。alloca 可能与结构化异常处理不兼容。有关使用 alloca 的限制,请参阅编译器手册。
C99 扩展支持可变大小的数组。这个特性是有争议的,并且只在 C 中可用,而不能在C++ 中使用。你可以使用 alloca 而不是可变大小的数组,因为它提供了相同的功能。
6.容器类
当使用动态内存分配,建议使用容器类,因为容器类有析构函数可以避免内存泄漏和空指针等问题。容器类还可以添加边界检查等功能。
可以使用c++STL标准模板库,然而STL的特点是通用性和灵活性,在内存分配时会浪费内存。如 list、set 和 map,甚至可能分配比容器中对象更大的内存块。STL deque(双向链表)为每四个对象分配一个内存块。STL vector 将所有的对象都存储在同一个内存块中,当这快内存被填满时会重新分配,这种情况经常发生,因为块大小每次只增长 50%或更少。针对vector,可以创建vector后调用vector::reserve重新分配预估的大小避免多次进行内存分配。其他 STL 容器没有预先分配内存的功能。
anger实现了一组示例容器类来提高效率www.agner.org/optimize/cppexamples.zip
在为特定用途选择容器时,应考虑以下因素:
- 包含一个还是多个元素?如果容器包含一个元素,那么可以使用智能指针(见7.9 智能指针)。
- 编译时是否知道大小?如果在编译时已知元素的数量,或者可以设置不太大的上限,那么最优解决方案是一个固定大小的数组或容器,而不需要动态内存分配。但是,如果数组或容器对于栈来说太大的时候,则可能需要动态内存分配。
- 在存储第一个元素之前,大小是否已知?如果在存储第一个元素之前可以知道元素的总数(或者有一个合理的估计),那么最好使用允许预先分配(
reserve)内存的容器,而不是分段分配内存或当内存块太小的时候重新分配。 - 对象是连续编号的么?如果对象是由连续的索引或有限范围内的键标识的,那么简单的数组是高效的解决方案。
- 对象是以先进先出的方式访问的么?如果在先进先出(FIFO)的基础上访问对象,则使用队列。将队列作为循环缓冲区而不是链表使用更高效。
- 对象是以先进后出的方式访问的么?如果对象是在先入后出(FILO)的基础上访问的,那么使用带有栈顶部索引的线性数组。
- 对象是由键标识的么?如果键值被限制在一个较窄的范围内,那么可以使用一个简单的数组。如果对象的数量很多,那么最高效的解决方案可能是二叉树或哈希图。
- 对象有顺序吗?如果你需要做这样的搜素:“离元素 x 最近的是哪个?”或者 “在 x 和 y之间有多少个元素?”,那么你可以使用有序列表或者二叉树。
- 添加所有对象之后是否需要搜索?如果需要搜索工具,但必须在容器中存储了所有对象之后,那么线性数组将是一个高效的解决方案。在添加所有元素之后对数组进行排序,然后使用二分搜索来查找元素。哈希表也可能是一种高效的解决方案。
- 添加所有对象之前是否需要搜索?如需要搜索工具,并且可以随时添加新对象,那么解决方案就更复杂了。如果元素的总数很少,那么有序列表是最高效的解决方案,因为它的简单。但是如果列表很大,有序列表会非常低效,因为在列表中插入一个新元素会导致所有后续元素都需要移动。在这种情况下我们需要二叉树或者哈希表。如果元素是有序的,并且在一定间隔后就会有搜素请求,那么可以使用二叉树。哈希表则可以在元素没有特定顺序但又唯一的键标识时使用。
- 对象是否具有混合类型或大小?可以在同一个内存池中存储不同类型的对象或不同长度的字符串。见 www.agner.org/optimize/cppexamples.zip。如果在编译时知道元素的数量和类型,那么就不需要使用容器或内存池。
- 是否要对齐?一些应用程序要求数据按可以被整除的地址对齐。特别是使用向量指令时,需要对齐的地址可以被 16整出。在某些情况下,将数据结构对齐到可被缓存线大小整除的地址(通常为64)可以提高性能。
- 是否使用多线程?如果多个线程可以同时添加、删除或修改对象,那么容器类通常不是线程安全的。在多线程应用程序中,为每个线程设置单独的容器要比临时锁定一个容器以供每个线程独占访问高效的多。
- 有指向包含的对象的指针么?将指针指向包含的对象可能是不安全的,因为容器可能在需要重新分配内存时移动对象。容器内的对象应该通过其在容器中的索引或键来标识,而不是通过指针或引用。但是,如果没有其他线程访问容器,则可以将指向此类对象的指针或引用传递给不添加或删除任何对象的函数。
- 容器可以被回收么?创建和删除容器的消耗很大。如果程序的逻辑允许,复用一个容器可能比删除它再重新创建一个更高效。
7.字符串
常用的字符串一般是char* string cstring char*是最原始的字符串,string是STL库中的,cstring是是包含一些C字符串的操作函数.
补充一下:包含头文件时,若有.h后缀表示是c的头文件,若没有.h后缀表示是cpp的头文件,同时cpp还有一些c开头的头文件,比如cmath,cstring,这意味着保留了c风格的cpp库
1 |
使用c风格的string处理函数如 strcpy、strcat、strlen、sprintf效率会高些。如果你想在不损害安全的情况下提高速度,你可以将所有字符串存储在内存池中,如上所述。anger手册的附录(www.agner.org/optimize/cppexamples.zip)中提供了示例
8.按顺序访问数据
这一小节其实是对cpu缓存的应用,当你按顺序访问数据时,cpucache命中会增多,程序效率就高,比如经典的行访问和列访问的例子。
1 | // Example 9.4 |
不要交换这两个循环的顺序(除非是在 Fortran 中,具有相反的存储顺序)。
9.在大数据结构中的缓存冲突
按顺序访问多维数组并不总是可能的。一些应用程序(例如,在线性代数中)需要其他访问模式。如果一个大矩阵中的行之间的距离恰好等于关键步长,就会导致严重的延迟,如9.2 缓存组织所述。如果矩阵行的大小(以字节为单位)是 2 的高次幂,就会发生这种情况。
下面的例子说明了这一点。我的例子是一个对二次矩阵进行转置的函数,即每个元素矩阵 [r][c] 与元素矩阵 [c][r] 交换。
1 | // Example 9.5a |
矩阵的转置和以对角线为轴做镜像是一样的。对角线以下的每个元素矩阵 [r][c] 在对角线以上的镜像位置与元素矩阵 [c][r] 交换。例 9.5a中的循环 c 从最左边的列到对角线。对角线上的元素保持不变。
这段代码的问题是,如果对角线以下的元素矩阵 [r][c] 是逐行访问的,那么对角线以上的镜像元素矩阵 [c][r] 是逐列访问的。
假设现在我们在奔腾4电脑上运行这段代码,矩阵的大小是 64。电脑的一级缓存为 8 kb = 8192 bytes,4 路,行大小为 64。每个缓存行可以保存8个 double 变量,每个变量的大小为8个字节。关键步长为 $8192/4=2048 bytes = 4 rows$。
让我们看看循环内部发生了什么,例如当 r = 28 时。我们从对角线以下的第 28行取出元素,并将这些元素与对角线以上的第 28列交换。第 28行中的前 8个元素共享同一缓存线。因为缓存线按行而不是按列缓存,在第 28列中的 8个元素将进入 8个不同的缓存行中。每四个高速缓存线属于同一组高速缓存。当我们操作到第 28列中的16号元素时,缓存将收回该列中0号使用的缓存线。17号元素将覆盖1号元素使用的缓存线,18号元素将覆盖 2号元素使用的缓存线,依此类推。这意味着当我们将第 29列与第 29行交换时,对角线以上使用的所有缓存线都被覆盖了。因为在我们需要下一个元素之前,它会被删除,每个缓存线必须重新加载 8次。我已经通过使用不同矩阵大小的奔腾4上的示例9.5a来测量转置矩阵所需的时间来证实这一点。我的实验结果如下,时间单位是每个数组元素所需要要的时钟周期。
| Matrix Size | Total kilobytes | Time per element |
|---|---|---|
| 63*63 | 31 | 11.6 |
| 64*64 | 32 | 16.4 |
| 65*65 | 33 | 11.8 |
| 127*127 | 126 | 12.2 |
| 128*128 | 128 | 17.4 |
| 129*129 | 130 | 14.4 |
| 511*511 | 2040 | 38.7 |
| 512*512 | 2048 | 230.7 |
| 513*513 | 2056 | 38.1 |
Table 9.1. Time for transposition of different size matrices, clock cycles per element.
从表中可以看出,当矩阵的大小是一级缓存大小的倍数时,转置矩阵要多花 40%的时间。这是因为关键步长是矩阵行的倍数。由于无序执行机制可以预先加载数据,延迟比一级缓存从二级缓存中重新加载数据的时间少。
当竞争发生在二级缓存中时,这种效果更为显著。二级缓存$512 kb$,8路。二级缓存的关键步长是$512 kb / 8 = 64 kb$。这对应于$512*512$矩阵中的16行数据。我在表 9.1中的实验结果表明,在二级缓存中发生竞争时,转置矩阵所需的时间是不发生竞争时的 6倍。这种效果在二级缓存竞争中比在一级缓存竞争中强得多的原因是二级缓存一次不能预加载多行。
解决这个问题的一个简单方法是使矩阵中的行比需要的长,以避免关键步长是矩阵行大小的倍数。我试着让矩阵的大小为$512*520$,包含不使用最后 8列。这消除了竞争,时间消耗减少到 36个时钟周期。
在某些情况下,不可能向矩阵中添加未使用的列。例如,一个数学函数库应该能够有效地处理所有大小的矩阵。在这种情况下,一个有效的解决方案是将矩阵分成更小的正方形,一次处理一个正方形。这被称为square blocking 或tiling。示例9.5b演示了这种技术:
1 | // Example 9.5b |
在我的实验中,使用这段代码,对于512*512的矩阵来说,每个元素消耗50个时钟周期。
二级缓存中竞争的代价是如此的昂贵,因此对它们采取措施非常重要。因此,你应该了解矩阵中列数为 2的高次幂的情况。一级缓存中的竞争消耗较少,可能不值得为了一级缓存中使用像square blocking这么复杂的技术。
Squre blocking以及类似的技术在 S. Goedecker 和 A. Hoisie 2001年出版的 “Performance Optimization of Numerically Intensive Codes”一书中有更详细的描述。