CMU 10-414/714 机器学习系统

lecture 0 机器学习数学基础

线性代数

空间：满足一定条件的集合

向量空间：定义了加法和数乘这两种运算的集合

向量：向量空间的元素

向量组：若干个同维数的列向量或行向量组成的集合叫做向量组

线性相关性：给定向量组A：a1,a2,a3,…,am，如果存在不全为零的λ1,λ2,…,λm使得λ1a1+λ2a2+…+λmam=0，则称A是线性相关的，反之则是线性无关。 ^8afaa2

内积：X点乘Y，即两个维数相同的向量每个对应的元素相乘，满足交换律，结合律，分配律

范数(Norm)：范数定义向量空间的距离，可以将向量映射到非负实数，用||x||来表示

L1范数：曼哈顿距离，一个元素中所有元素绝对值之和，||x||1= |x1| + |x2| + … + |xn|

L2范数：欧几里得范数（Euclidean Norm），定义为向量各元素平方和的平方根，记作 ||x||2。对于n维向量x=[x1, x2, …, xn]，其L2范数为：||x||2 = sqrt(x1^2 + x2^2 + … + xn^2)

内积的几何解释：image-20230726144821388

线性变换：向量空间的向量通过一个矩阵进行变换

具体来说，设V和W是两个向量空间，T是从V到W的一个映射，如果满足以下两个条件，则称T是一个线性变换：

  1. 齐次性：对于任意的向量u和标量k，有T(ku) = kT(u)。
  2. 可加性：对于任意的向量u和v，有T(u + v) = T(u) + T(v)

线性变换具有很多重要的性质，例如：

  1. 线性变换保持向量空间的加法和标量乘法，即对于任意的向量u和v，标量k，有T(u + v) = T(u) + T(v)，T(ku) = kT(u)。 ^8d1559
  2. 线性变换可以通过矩阵乘法来表示，即T(u) = Au，其中A是一个m×n的矩阵。
  3. 线性变换可以通过矩阵的特征值和特征向量来描述，特别地，如果矩阵A有n个线性无关的特征向量，则可以将A对角化为对角矩阵，从而简化线性变换的计算。

矩阵运算：矩阵相乘是两种线性变换的叠加！

矩阵的逆：对于一个n×n的矩阵A，如果存在一个n×n的矩阵B，使得AB=BA=I（其中I是n阶单位矩阵），则称矩阵A是可逆的，而B就是A的逆矩阵，记作A^-1。如果矩阵A不可逆，则称其为奇异矩阵
在几何上，一个矩阵的逆矩阵就是该矩阵的反运动。

特征值和特征向量：对于一个n×n的矩阵A，如果存在一个非零向量v和标量λ，使得Av=λv，则称λ是矩阵A的一个特征值，v是对应于特征值λ的特征向量。一个矩阵可以有1个或多个特征值和对应的特征向量。 ^edaa57

对称矩阵：指的是一个矩阵A，满足A的转置矩阵等于A本身。

正定矩阵：指的是一个对称矩阵A，满足对于任意非零向量x，均有x^T Ax > 0，即A的所有特征值都是正的。

微积分

函数，反函数，复合函数：太基础了

导数：image-20230726151625656

导数的和差积商和复合函数求导法则

高阶导数：二阶及以上的导数

偏导数： 二元函数和多元函数具有偏导数，求偏导，把除了要导的变量以外的其他变量看作常数进行求导

方向导数：

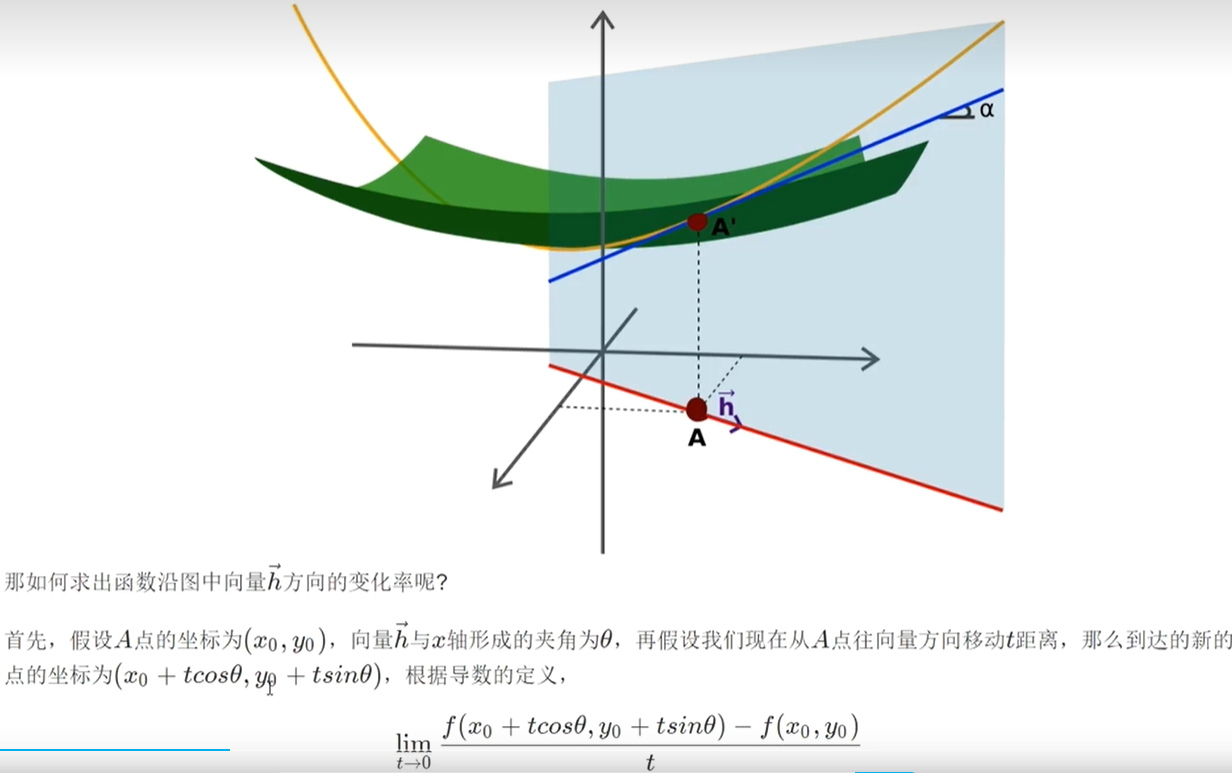
image-20230726153344561

梯度：描述了多元函数在某一点上升最快的方向和速率，于一个n元函数f(x1, x2, …, xn)，在点P(x1, x2, …, xn)处的梯度向量表示函数在该点上升最快的方向和速率，通常记作∇f(P)。

梯度向量的定义是：

∇f(P) = (df/dx1, df/dx2, …, df/dxn)

其中，df/dxi表示函数f(x1, x2, …, xn)对变量xi的偏导数。梯度向量的方向是函数在该点上升最快的方向，它的模长表示函数在该点上升的速率。

image-20230726153556091

关于全微分和偏微分：

image-20230726155205157

雅可比矩阵：

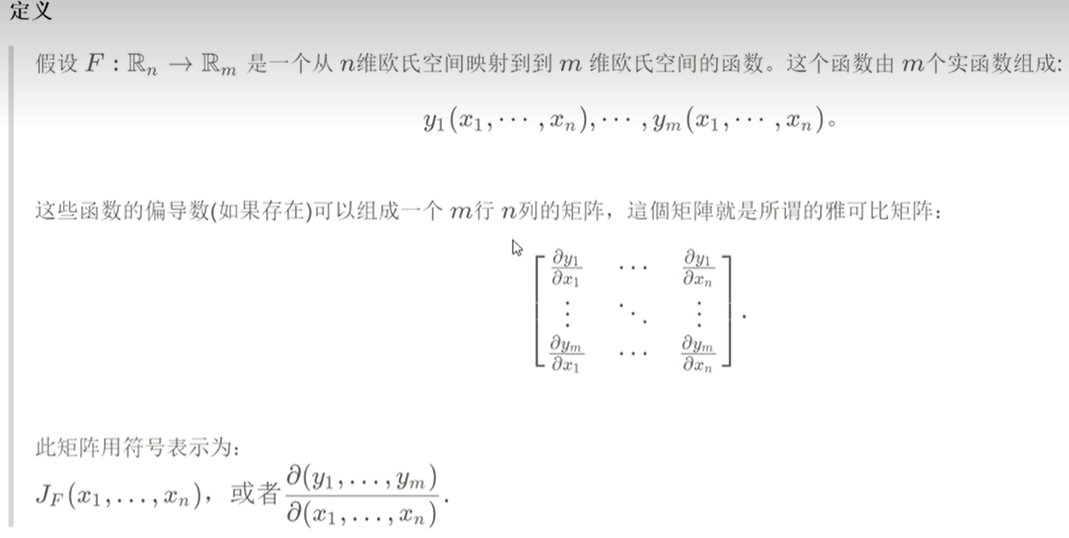
image-20230726154602944

雅可比矩阵和梯度向量：

从定义上来看，雅可比矩阵和梯度都是描述函数在某一点的偏导数信息。但是它们的表示形式和用途有所不同。雅可比矩阵是一个矩阵，它的每一行都表示函数对某个变量的偏导数，用于描述函数在某一点的变化率和方向；而梯度是一个向量，它的每个分量都表示函数对某个变量的偏导数，用于描述函数在某一点上升最快的方向和速率。

梯度向量与雅可比矩阵之间存在一定的联系。在某一点x处，函数f(x1, x2, …, xn)的梯度向量可以表示为对应的雅可比矩阵的转置与输入向量的乘积，即：

∇f(x) = J(x)^T · v

其中，v是一个n维向量，表示方向向量。这个式子的意义是：如果我们在点x处沿着向量v的方向移动，那么函数f(x1, x2, …, xn)在该点上升的速率最大，且上升最快的方向与梯度向量的方向相同。

lecture 1 简介

lecture2 ML Refresher / Softmax Regression

每个机器学习算法包含三个不同的元素：

  • 假设类：通过一系列参数描述我们希望怎样将input映射到output。
  • 损失函数：指定了什么是好的假设
  • 优化方法：通过优化参数来减少训练集上的损失总和

symbol

  • n：输入数据的维数
  • k：预测分类或者label的数量
  • m：训练集中元素数量

例如 minist中

  • n：28*28=784像素
  • k：10个分类
  • m：6000个样本

以线性回归为例：

假设函数：$\theta$是一个n * k 矩阵，通过矩阵乘将向量X从n维映射到K维

image-20230726191705162

损失函数：
比如可以选择分类错误率作为损失函数

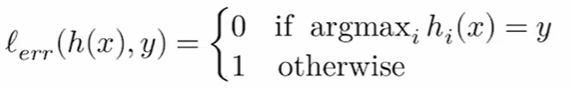
image-20230726192124540

然而这种损失函数对优化非常不利，很难找到最小化这种误差损失的参数

再来看另一种损失函数，softmax

通过指数化(e的幂次方将数字变正)和归一化将假设函数转换成概率

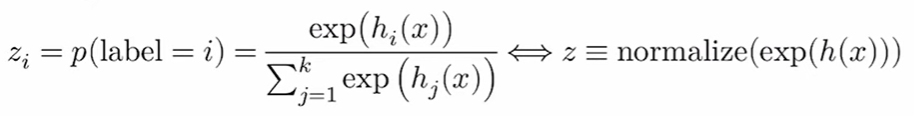
image-20230726193559993

此时概率高的就是好的假设，所以损失函数可以表示为：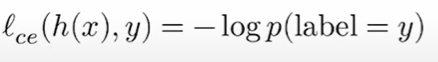
image-20230726194018167

进一步化简image-20231122162246486

也就是交叉熵损失函数，概率越高，损失越小

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def softmax_loss(Z, y):
    """ Return softmax loss.  Note that for the purposes of this assignment,
    you don't need to worry about "nicely" scaling the numerical properties
    of the log-sum-exp computation, but can just compute this directly.

    Args:
        Z (np.ndarray[np.float32]): 2D numpy array of shape
            (batch_size, num_classes), containing the logit predictions for
            each class.
        y (np.ndarray[np.uint8]): 1D numpy array of shape (batch_size, )
            containing the true label of each example.

    Returns:
        Average softmax loss over the sample.
    """
    #针对输入首先计算指数
    exp_Z = np.exp(Z)
    #然后计算softmax，具体做法就是每一个batch的指数化元素除以这些元素的和
    #计算和使用sum函数，axis=1即可
    softmax=exp_Z/np.sum(exp_Z,axis=1,keepdims=True)
    #然后利用softmax计算损失函数，
    #首先要得到每个批次的损失函数，计算方法是先得到softmax中真实标签的概率，将其log并取负
    num_batchs=Z.shape[0]
    #特别说明这里的list索引操作，要得到softmax中每个批次对应真实标签的概率，二维数组的第一个索引应该是batch数，从0到num_batchs，第二个标签是y的值，python支持这种索引方式
    loss=-np.log(softmax[np.arange(num_batchs),y])
    #然后求平均损失函数，就是相加除以批次数即可
    avg_loss=np.sum(loss)/sum_batchs

优化方法：

针对上面的假设函数和损失函数，其优化方法可以表示为：

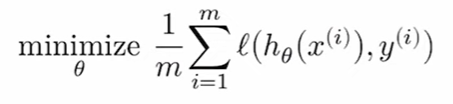
image-20230726194959228

即找到最佳的θ，使得右边的公式最小。(对训练集中的每一个元素的损失函数的平均值最小)

最通用的优化方法：梯度下降

梯度：函数的偏导数矩阵image-20230726195658879

梯度指向了f增大最快的方向，所以为了最小化一个函数，梯度下降算法在负梯度的方向上迭代的采取行动，通常为θ减去α倍的梯度矩阵，α就是学习率。

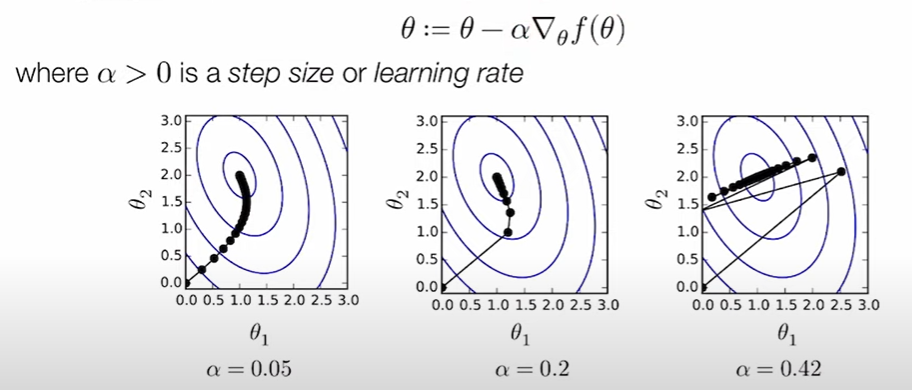
image-20230726200341215

随机梯度下降(stochastic gradient descent,SGD)

直接使用所有样本的数据计算梯度对参数进行一次更新是不现实的，一方面计算所有样本的梯度需要极大的内存和算力，另一方面进行一次更新无法进行良好的优化。所以我们我们把样本分批次计算多次梯度，更新多次参数。

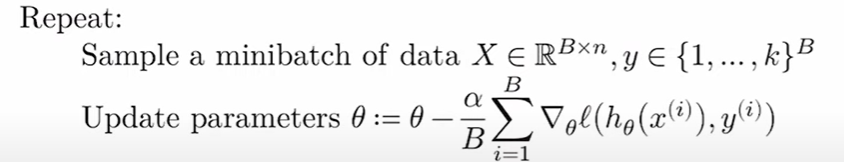
image-20230726201324748

整合一下：

重复以下过程直到参数或者损失收敛

  1. 迭代训练集的小批次
  2. 更新参数θ

softmax的随机梯度下降

要计算损失函数的梯度，softmax有一个巧妙的变换

$$∇Θℓsoftmax(ΘTx,y)=x(z−ey)T$$

z是归一化的softmax，ey是一个全是0的向量，在y的位置有一个1。

表现在代码上：softmax对应标签的概率-1即为梯度

1
2
3
4
# 计算当前批次的梯度
    grad = softmax.copy()
    grad[np.arange(batch), y_batch] -= 1
    grad /= batch

然后更新theta的时候要注意数据维度要一样，用X的转置乘梯度得到真正的梯度

1
theta -= lr * np.dot(X_batch.T, grad)

lecture3 “Manual” Neural Networks

线性分类处理线性可分问题。对于非线性可分问题：

普通的线性分类不可行，可以通过映射函数将输入转换到高维空间再进行线性分类，也就是核方法。

还有另一种方法：

即将 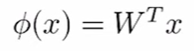image-20230726165832998到image-20230726165847090

假设σ是某个非线性函数，W是随机的矩阵，可以通过优化W来减少损失，这就是神经网络要做的事。

神经网络是假设类的一种特殊形式。

两层神经网络：

image-20230726171303234

这个两层的神经网络将输入的x乘W1矩阵，以及σ函数变换得到新的数据，在经过W2矩阵得到输出

L层神经网络：

image-20230726173120375

有L个矩阵W，输入经过L层W矩阵和非线性函数得到输出

一个简单的神经网络例子：

  • 损失函数依旧为交叉熵损失
  • 优化方法依旧为随机梯度下降SGD

只是假设函数现在是神经网络了。

image-20230726204037941

在线性回归中，每次更新θ即线性公式的参数，而在神经网络中，更新的θ即为神经网络每层的参数(即每层每个节点的参数)。在求第i层参数的梯度时，需要把第i+1层的参数作为常数，也就是依赖i+1层的参数，所以我们需要从最后一层开始计算，然后一层一层向前传播，这就是反向传播

前向传播计算输出，反向传播计算梯度。

image-20230726211347711

前向传播的Zi和反向传播的Gi都要缓存

lecture 4 automatic differentiation

关于微分

  • 符号微分：根据求导法则对表达式进行变换：数值结果精准但是表达式膨胀
  • 数值微分：使用有限差分进行近似：容易实现，但是计算结果不精准，复杂度高。对h要求高
  • 自动微分：所有的数值计算都由有限的基本运算组成，而基本运算的导数表达式是已知的，通过链式法则将数值计算各部分组合成整体。

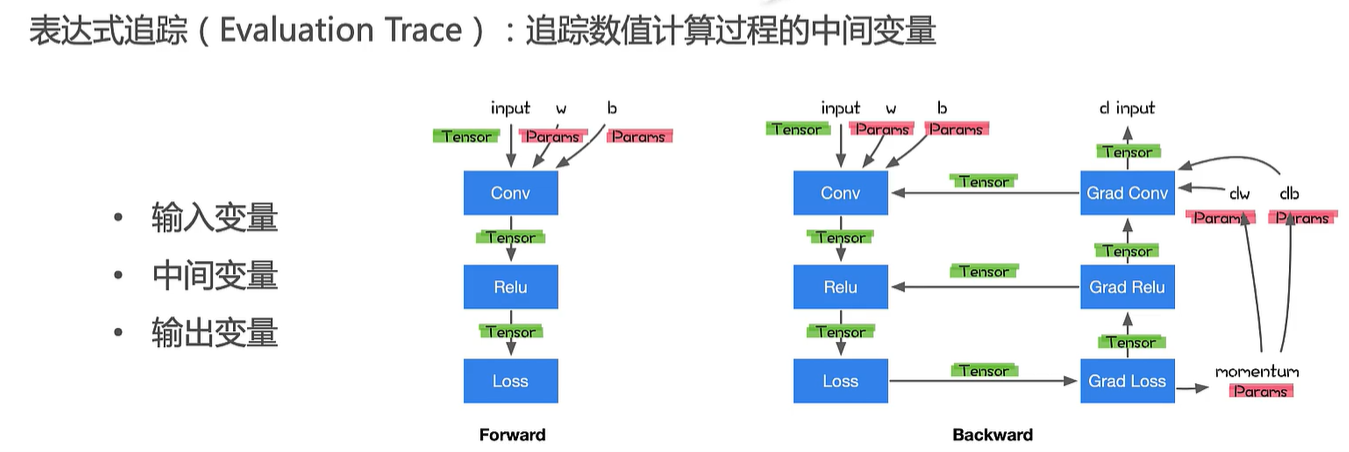
image-20230725200408335

通过计算图来实现自动微分

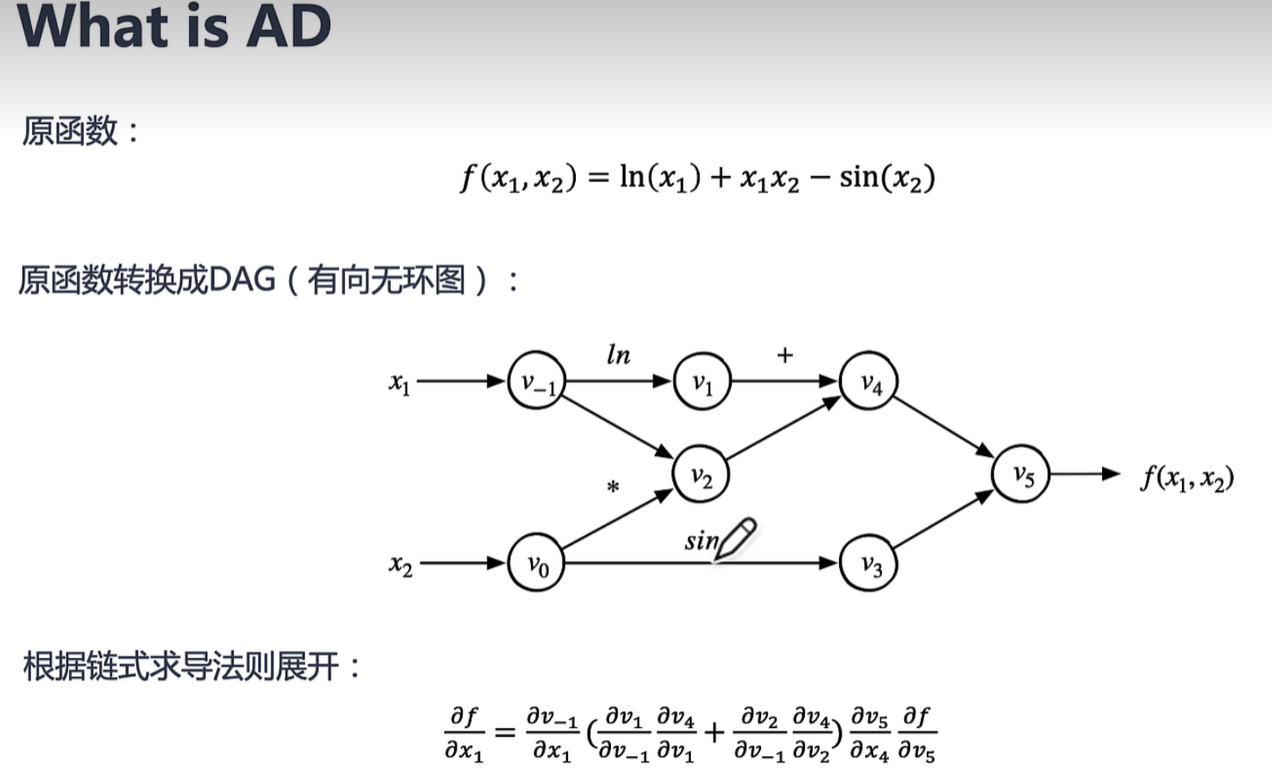
image-20230725201439683

正向自动微分：利用链式法则一步步求偏导

正向：v1->x1 v2->x1 …… vn->x1 y->x1

反向：y->vn y->vn-1 …… y->v1 y->x

image-20230726222658274

设输入为N输出为K，当N小K大时，正向自动微分会很好用，但是神经网络通常具有大量输入和较少输出，所以更适用反向自动微分

反向自动微分

image-20230725202259219

image-20230726222723308

需要注意的是多路径的情况，要将两个伴随值加起来才能得到前面变量的伴随值。

image-20230726220429091

代码

image-20230726220739785

先创建字典存储反向计算图的节点，然后从最后开始遍历反向计算图的拓扑序列，计算i的partial adjoint时依赖的是i到后面节点的partial adjoint，(最初的可以直接得到，后面的可以在下面的循环都计算出来)，算出i的partial adjoint后，再在内层循环计算所有从k到i节点的partial adjoint（这将会在后面的外层循环用到），将其加入字典。然后外层循环结束后就会计算出所有节点的partial adjoint。

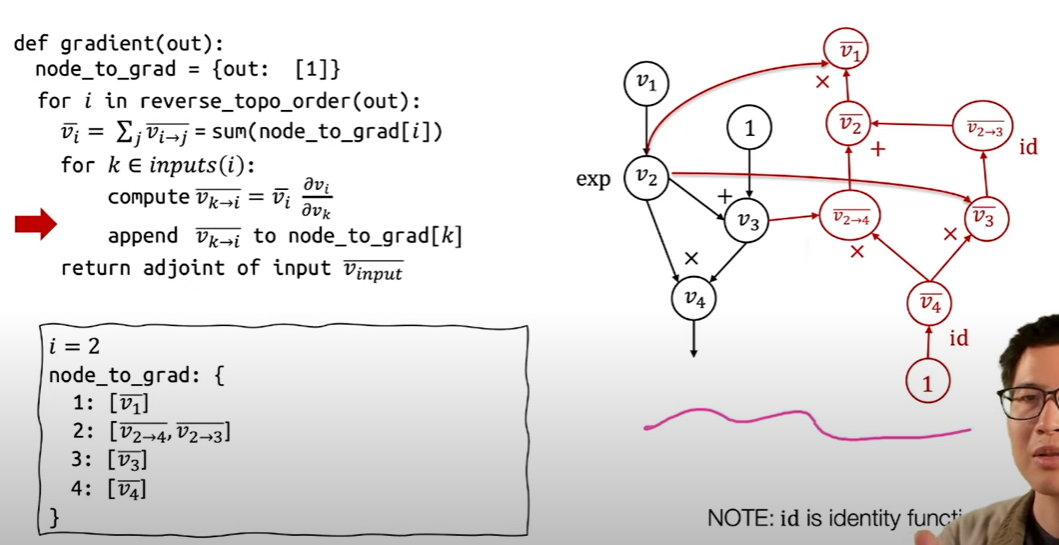
image-20230727145958762

reverse mode AD的优点

  • 通过原始的计算图反向自动微分时又创建了新的计算图，从而可以再次微分，计算微分的微分。
  • 自动微分时创建的新的计算图可以帮助优化，比如算子融合等等，虽然前向计算和梯度计算不对称，但是梯度计算会更快。

reverse mode AD on tensors

在神经网络中，每一层的参数通常是张量，将反向自动微分推导到张量也很简单，只需要定价伴随值为矩阵或张量的形式即可，求伴随值和之前类型，可以表达为矩阵形式

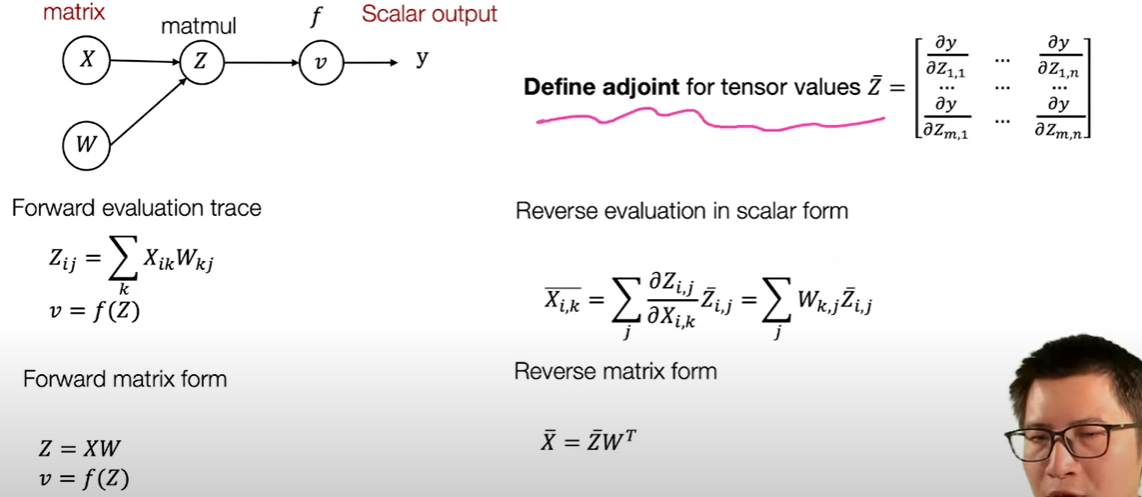
image-20230726222030884

reverse mode AD on data structures

如果中间层不是张量，而是字典这种数据结构呢？

image-20230726222618167

lecture 5 Automatic Differentiation Implementation

colab运行时间太久内核会损坏，要重启内核

  1. import os
  2. os.kill(os.getpid(), 9)

Value类代表计算图的节点，记录cached_data，输入的value，和当前节点所作的Op

Op类代表操作类

在Tensor执行计算Op时，会进入__call__方法，进而进入make_from_op方法，这个方法创建计算图节点

1
2
3
4
5
6
7
@staticmethod
def make_from_op(op: Op, inputs: List["Value"]):
    tensor = Tensor.__new__(Tensor)
    tensor._init(op, inputs)
    if not LAZY_MODE:
        tensor.realize_cached_data()
    return tensor

调用_init方法初始化tensor。如果不是LAZY_MODE就计算realize_cached_data

真正的计算不会发生直到realize_cached_data被调用

detach()返回一个计算图之外的新的Tensor

Ops里定义各种算子，主要有compute和gradient两个函数，一个计算值，一个计算梯度

1
2
3
def gradient(self, out_grad: Tensor, node: Tensor):
    lhs, rhs = node.inputs
    return out_grad * rhs, out_grad * lhs

参数out_grad是后面节点的adjoint，然后乘上该Op的偏导，比如这里是乘法就是把常数保留下来。

Lecture 6 Fully connected networks,optimization,initialization

广播代替偏置变量，广播将n*1的向量自动拓展成n*p的矩阵，

广播不会复制任何数据

优化方法：

除了随机梯度下降，其他的优化方法

牛顿方法

相比于SGD，牛顿方法能准确找到正确的优化方向，不会像SGD一样有反弹

然而，由于hessian矩阵太大，乘法微分开销太大

牛顿方法（Newton’s method）是一种用于求解方程或最小化函数的迭代方法。它的基本思想是利用函数的一阶和二阶导数信息来不断逼近函数的根或极小值点。

在求解一个方程 $f(x)=0$ 的根时，牛顿方法通过不断迭代下面的公式来逼近根：

$$x_{n+1} = x_n - \frac{f(x_n)}{f’(x_n)}$$

其中，$x_n$ 是第 $n$ 次迭代得到的根的估计值，$f(x)$ 和 $f’(x)$ 分别是函数 $f(x)$ 在 $x$ 处的函数值和一阶导数值。通过不断迭代这个公式，我们可以逐步逼近函数的根。

在求解一个函数的极小值点时，牛顿方法通过不断迭代下面的公式来逼近极小值点：

$$x_{n+1} = x_n - \frac{f’(x_n)}{f’’(x_n)}$$

其中，$f(x)$ 和 $f’(x)$ 分别是函数 $f(x)$ 在 $x$ 处的函数值和一阶导数值，$f’’(x)$ 是函数 $f(x)$ 在 $x$ 处的二阶导数值。通过不断迭代这个公式，我们可以逐步逼近函数的极小值点。

需要注意的是，牛顿方法只能保证在函数充分光滑且初值足够接近真实解时收敛，否则可能会出现发散或收敛到错误的根或极值点的情况。因此，牛顿方法的使用需要谨慎，并且需要根据具体问题和函数的特性进行调整和优化。

Hessian 矩阵是一个二次偏导数矩阵，它是多元函数的二阶导数矩阵。对于一个 $n$ 元函数 $f(x_1, x_2, …, x_n)$，它的 Hessian 矩阵 $H$ 定义为：

$$H_{i,j} = \frac{\partial^2 f}{\partial x_i \partial x_j}, \quad i,j = 1,2,\ldots,n$$

Hessian 矩阵是一个 $n \times n$ 的矩阵，其中第 $i$ 行第 $j$ 列的元素表示对 $x_i$ 取二阶偏导数再对 $x_j$ 取偏导数的结果。因此，Hessian 矩阵是一个对称矩阵。

Momentum动量

Momentum 是一种优化算法，它是基于梯度下降算法的改进版。Momentum 的基本思想是在梯度下降的基础上引入动量（momentum）的概念，以加速优化过程并减少震荡。

具体来说，Momentum 算法在每次迭代时，不仅利用当前的梯度信息更新参数，还引入一个动量变量，用于记录之前的梯度信息。具体实现时，Momentum 算法会维护一个动量向量 $v$，并在每次迭代时使用以下公式更新参数：

$$v_{t+1} = \beta v_t + (1-\beta) \nabla_\theta J(\theta)$$

$$\theta_{t+1} = \theta_t - \alpha v_{t+1}$$

其中，$\theta$ 表示模型的参数，$J(\theta)$ 表示损失函数，$\nabla_\theta J(\theta)$ 表示损失函数关于参数的梯度，$\alpha$ 表示学习率，$\beta$ 表示动量参数，通常取一个介于 0 到 1 之间的值。在每次迭代时，Momentum 算法会将当前梯度和之前的动量相结合，然后用加权平均的方式更新动量向量 $v$。在下一次迭代时，Momentum 算法会利用更新后的动量向量计算参数的更新量，并进行参数更新。

Momentum 算法的引入可以有效减少震荡，加速收敛速度。当梯度在某个方向上连续变化时，动量可以将参数更新方向保持在这个方向上，从而加速收敛。同时，动量也可以减少梯度在垂直方向上的震荡，从而避免参数更新过程中出现来回跳动的情况。

unbiasing momentum 去偏

在使用 Momentum 算法进行优化时，由于动量变量会不断累积之前的梯度信息，因此可能会导致动量变量的估计值存在一定的偏差。这种偏差可能会影响优化的收敛性和稳定性。为了解决这个问题，可以使用 unbiasing（去偏）技巧对动量变量进行修正，从而得到更准确的动量估计。

具体来说，在 Momentum 算法中，动量变量 $v_t$ 可以被看作是历史梯度的加权平均值。当动量参数 $\beta$ 较小时，动量变量会受到之前梯度的影响较大，因此可能会存在较大的偏差。为了解决这个问题，可以使用 unbiasing 技巧对动量变量进行修正，得到无偏的动量估计。具体实现时，可以使用以下公式对动量变量进行修正：

$$\hat{v}_t = \frac{v_t}{1-\beta^t}$$

其中，$\hat{v}_t$ 表示修正后的动量变量，$v_t$ 表示原始的动量变量，$t$ 表示当前迭代次数，$\beta$ 表示动量参数。

所以最终梯度更新变为$$\theta_{t+1} = \theta_t - \alpha v_{t}/(1-\beta^{t+1})$$

Nesterov Momentum

Nesterov Momentum（Nesterov 加速梯度下降算法，也称为 Nesterov Accelerated Gradient，NAG）是 Momentum 算法的一种改进版本，它可以更快地收敛并且通常比标准的 Momentum 算法表现更好。

Nesterov Momentum 的基本思想是在 Momentum 算法的基础上引入 Nesterov 更新（Nesterov update）的概念，以更准确地估计参数更新的方向。具体来说，Nesterov Momentum 在计算梯度时，会先根据当前的动量变量 $v_t$ 估计下一次迭代时的参数值 $\theta_{t+1}$，然后再在这个位置计算梯度，最后根据修正后的梯度更新动量变量和参数。具体实现时，Nesterov Momentum 的更新公式为：

$$v_{t+1} = \beta v_t + (1-\beta) \nabla_\theta J(\theta - \beta v_t)$$

$$\theta_{t+1} = \theta_t - \alpha v_{t+1}$$

其中，$\theta$ 表示模型的参数，$J(\theta)$ 表示损失函数，$\nabla_\theta J(\theta)$ 表示损失函数关于参数的梯度，$\alpha$ 表示学习率，$\beta$ 表示动量参数。在每次迭代时，Nesterov Momentum 会先使用当前的动量变量 $v_t$ 来估计下一次迭代时的参数值 $\theta_{t+1}$，然后在这个位置计算梯度，最后根据修正后的梯度更新动量变量和参数。

相比于标准的 Momentum 算法，Nesterov Momentum 引入了 Nesterov 更新的概念，可以更准确地估计参数更新的方向，从而提高了优化的收敛速度和稳定性。需要注意的是，在实际应用中，我们需要根据具体问题和数据集的特性，选择合适的优化算法，并进行合理的超参数设置。

Adam

Adam（Adaptive Moment Estimation）是一种自适应学习率优化算法，在深度学习中被广泛应用。Adam 算法结合了动量梯度下降和自适应学习率的优点，能够快速、稳定地收敛，并且对超参数的选择相对不敏感。

Adam 算法的基本思想是在梯度下降的基础上引入动量变量和自适应学习率，以解决传统梯度下降算法中学习率难以确定的问题。具体来说，Adam 算法会维护一个动量变量 $m_t$ 和一个二阶矩变量 $v_t$，并在每次迭代时使用以下公式更新它们：

$$m_t = \beta_1 m_{t-1} + (1-\beta_1) \nabla_\theta J(\theta_{t-1})$$

$$v_t = \beta_2 v_{t-1} + (1-\beta_2) (\nabla_\theta J(\theta_{t-1}))^2$$

其中，$\theta$ 表示模型的参数，$J(\theta)$ 表示损失函数，$\nabla_\theta J(\theta)$ 表示损失函数关于参数的梯度，$\beta_1$ 和 $\beta_2$ 分别表示动量变量和二阶矩变量的衰减系数，通常取一个介于 0 到 1 之间的值。在每次迭代时，Adam 算法会使用动量变量和二阶矩变量的估计值来计算一个自适应学习率，然后用这个学习率更新参数：

$$\hat{m}_t = \frac{m_t}{1-\beta_1^t}$$

$$\hat{v}_t = \frac{v_t}{1-\beta_2^t}$$

$$\theta_t = \theta_{t-1} - \frac{\alpha}{\sqrt{\hat{v}_t}+\epsilon} \hat{m}_t$$

其中，$\hat{m}_t$ 和 $\hat{v}_t$ 分别表示修正后的动量变量和二阶矩变量，$\alpha$ 表示初始学习率，$\epsilon$ 是为了数值稳定性而添加的小常数，通常取一个很小的值。

初始化权重

如何初始化参数Wi, bi? 初始化为0是不利于优化的

初始化的选择是非常重要的，对网络的行为和性能产生很大的影响。在网络运行时权重变化的并不大，因此初始化非常重要

Kaiming正态分布初始化（Kaiming Normal Initialization），又称He正态分布初始化，是一种用于初始化神经网络权重的方法。它是由Kaiming He等人在2015年提出的，是一种针对于ReLU激活函数而设计的初始化方法。

在神经网络中，权重的初始化通常会影响模型的收敛速度和性能。传统的初始化方法如随机初始化或者Xavier初始化，可能会导致梯度消失或者梯度爆炸的问题，特别是在深度神经网络中更为明显。为了解决这个问题，Kaiming等人提出了一种特别为ReLU激活函数设计的初始化方法。

Kaiming正态分布初始化的思想是，对于ReLU激活函数来说，当权重初始化为正态分布时，应该使得输入和输出的方差尽可能相等。具体来说，Kaiming正态分布初始化会生成一个均值为0，标准差为$\sqrt{\frac{2}{n_{in}}}$的正态分布，其中$n_{in}$表示该神经元的输入维度。这个标准差的设定来自于ReLU函数的导数的方差为$\frac{1}{2}$，因此对于一个有$n_{in}$个输入的神经元，其输入的方差为$n_{in}$倍，因此需要将标准差设为$\sqrt{\frac{2}{n_{in}}}$。

需要注意的是，Kaiming正态分布初始化适用于ReLU激活函数，对于其他的激活函数，可能需要使用其他的初始化方法。此外，对于深度神经网络，还需要注意合理设置各层之间的连接权重，以避免梯度消失或者梯度爆炸的问题。

Lecture 7 Neural Network Abstractions

caffe：定义layer类，包含forward和backward方法，表示前向传播和反向传播，没有自动传播

tensorflow：命令式编程，创建变量，定义变量之间关系，启动session，使用session去run这个计算过程

image-20230814164418604

优势：如果想的话可以只进行部分计算，减少计算。使用session可以开启远程会话

pytorch(needle)：命令式编程，与tensorflow的区别是，pytorch是定义并且运行，而tensorflow是分开的

image-20230814165200823、

这种方法的好处是可以动态的构建计算图，如上图所示通过ifelse判断语句来决定计算过程

从优化角度来说，tensorflow更加友好，但是pytorch对编程更友好（静态图与动态图）

dlsys的元素

  • module
  • loss function
  • optimizer
  • initialization
  • data loader and preprocessing

深度学习模块

module：张量进，张量出

loss function也是一种module，张量进，标量出

optimizer：即优化方法，通过SGD,SGD with momentum,Adam等方法优化权重

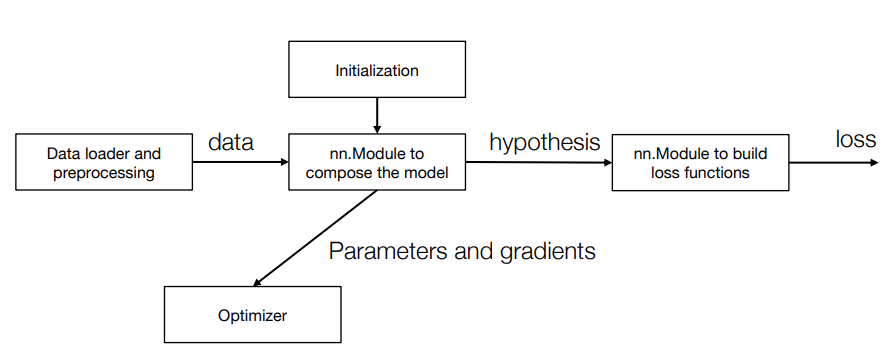
image-20230814172722075

Lecture 8 - Neural Network Library Implementation

之前的代码直接张量计算，每个tensor都包含计算图的信息，这是非常冗余的，且可能会造成out of memory错误。

解决这个问题可以使用detach函数创建只含有数据不含计算图信息的张量（op inputs）。

可以通过data属性访问这个副本

在计算时，询问自己是否需要构建计算图，不需要就用detach

由于浮点数尾数限制，太大的数无法表示，解决方法就是统一减去相同的常量，在softmax中，可以通过减去一个相同的常量来避免

image-20231122214442937

引入module

引入optimizer

Lecture 9 - Normalization and Regularization

Normalization

初始化

回顾一下正态分布

概率曲线在均值处达到最大，并且对称

标准差决定曲线的陡峭成都，标准差越小意味着大多数变量离均数越近，标准差越大越分散

若使用正态分布来初始化参数，Wi~N(0,c/n)，c/n的大小会有显著影响

image-20231123143219037

大的会炸精度，小的没效果

参数初始化十分重要，权重参数会影响激活函数和梯度变化

而且在训练过程中，激活函数和梯度都有较大变化，但是权重参数基本没有变化

layer normalization

在深度学习中，归一化（Normalization）是一种常用的数据预处理技术，旨在将输入数据调整到统一的尺度范围内，以提高模型的训练效果和稳定性。

归一化的主要目的是消除输入数据之间的尺度差异，使得不同特征的取值范围相近或相同。这对于许多机器学习算法来说是非常重要的，因为如果特征的尺度差异过大，可能会导致模型在训练过程中收敛困难，影响模型的性能。

常见的归一化方法包括以下几种：

  1. 均值归一化（Mean Normalization）：将数据减去其均值，使得数据的均值为0。这样可以消除数据的偏移，使得数据围绕着0中心变化。
  2. 标准化（Standardization）：也称为Z-score归一化，将数据减去均值并除以标准差，使得数据的均值为0，标准差为1。标准化可以消除数据的偏移和尺度差异，使得数据符合标准正态分布。
  3. 最大最小值归一化（Min-Max Normalization）：将数据线性映射到一个指定的最小值和最大值之间的范围，通常是[0, 1]或[-1, 1]。这样可以将数据压缩到一个固定的区间，保留了数据的相对顺序关系。
  4. L2归一化（L2 Normalization）：也称为向量的单位化（Unit Vector），将数据向量除以其L2范数，使得数据向量的长度为1。L2归一化可以将数据投影到单位球面上，保留了数据向量的方向信息。

对每一层的激活函数进行标准化（均值为0，方差为1），这就是所谓的层规范化

  1. 对于每个特征，计算该特征在整个数据集上的均值（mean）和标准差（standard deviation）。
  2. 对于每个特征值，减去均值，然后除以标准差。（var就是标准差，伊普西隆是小常数，避免除零）

image-20231123144811434

然而在实践中，对全连接网络很难训练得到低损耗的网络

batch normalization

批归一化（Batch Normalization）是一种应用于深度神经网络中的归一化技术。与传统的归一化方法不同，批归一化是基于每个小批量数据进行归一化操作，而不是对整个数据集进行归一化。

批归一化的主要思想是在神经网络的每个隐藏层之后，对每个小批量数据进行归一化处理，以使得各层的输入保持在较稳定的范围内。具体而言，对于每个输入特征，批归一化通过以下步骤进行操作：

  1. 对于给定的小批量数据，计算该批量数据在每个特征上的均值和方差。

  2. 使用计算得到的均值和方差对批量数据进行标准化，将数据中心化并缩放为单位方差。

  3. 应用可学习的缩放参数和偏移参数，对标准化后的数据进行线性变换，以恢复数据的表示能力。

批归一化的优点包括：

  1. 加速训练收敛：批归一化可以使得每层的输入保持在相对稳定的范围内，有助于加速模型的收敛速度，减少训练所需的迭代次数。

  2. 提高模型泛化能力：批归一化可以减少不同批次之间的内部协变量偏移（Internal Covariate Shift），有助于模型更好地学习特征，并提高模型的泛化能力。

  3. 减少对初始参数的敏感性：批归一化对网络中间层的参数初始化相对不那么敏感，使得初始化参数的选择范围更大，简化了模型的设计和调试过程。

需要注意的是，在使用批归一化时，通常会将批归一化层放置在激活函数之前，即在激活函数之前对输入进行归一化处理。此外，批归一化在训练和推理阶段的计算方式略有不同，但其核心思想是一致的。

批归一化已经成为深度学习中广泛应用的技术，并在许多网络结构和任务中取得了显著的性能提升。

不归一化行，而是归一化列

image-20231123150222363

image-20231123150240391

Regularization

过拟合 泛化能力差，正则化解决这个问题。正则化分隐式和显式，隐式比如SGD

L2 regularization aka weight decay

通常，模型参数的大小通常是复杂性的合理代表，因此我们可以在保持参数较小的同时最小化损失

参数越小，函数越平滑，可以通过

image-20231123151620984

dropout

Dropout是一种常用的正则化技术，用于减少深度神经网络中的过拟合现象。它在训练过程中以一定的概率丢弃（将其置零）网络中的神经元，从而降低神经网络对特定神经元的依赖性，增强网络的泛化能力。

具体来说，Dropout 在每次训练迭代中以一定的概率（通常为0.5）随机丢弃隐藏层的神经元。这意味着每个神经元都有一定的概率被临时忽略，其输出值为零。在进行下一次迭代时，又随机选择一部分神经元进行丢弃，这样不同的神经元组合形成了不同的子网络。

通过随机丢弃神经元，Dropout 可以防止神经元之间形成复杂的共适应关系，使得网络不依赖于特定的神经元，从而减少过拟合的风险。它相当于训练了一个包含了所有子网络的集成模型，每个子网络都是通过保留一部分神经元并丢弃其他神经元而得到的。

在测试或推理阶段，Dropout 不会被应用，而是通过对每个神经元的输出值乘以保留概率来进行缩放，以保持期望的输出值。

image-20231123152518021

将dropout和随机梯度下降类似

image-20231123152753498

Lecture 10 - Convolutional Networks

卷积

全连接网络将输入图片看作向量，当图片像素变多时，这个向量维度将会很大，相应的参数也会很多

通过卷积操作将子矩阵映射为一个元素，从而减少维数

image-20231127145138639

卷积：使用卷积核以滑动窗口的方式在输入数据上进行扫描，并计算出每个位置上的卷积操作结果

神经网络中的卷积时多通道卷积，映射多通道输入到多通道隐藏单元

将输入输出数据看作矩阵，size是h*w ，每一个元素代表一个长度为C的向量

image-20231127151121439

padding

只是对原始图像做卷积得到的输出比原始图像小，可以通过padding的方法，用0填充原始图像的周围（对于size为K的卷积核，填充(k-1)/2个零），使得到的输出和原始图像大小相同

降维：pooling strided convolutions

池化包括最大最小、平均池化等，只取部分元素

跨步卷积：卷积的时候一次跨stride 移动

grouped convolution

不再全通道都做卷积，而是分组做卷积

image-20231127154128046

Dilations（扩张）

张卷积（Dilated Convolution）是一种修改过的卷积操作，通过在卷积核的元素之间插入零值，使得卷积核在输入数据上可以跳过一定数量的像素进行计算。

通过调整扩张率（Dilation Rate）的大小，可以控制卷积操作的感受野（Receptive Field）大小和输出特征图的分辨率。较小的扩张率会导致较小的感受野和较高的分辨率，而较大的扩张率会导致较大的感受野和较低的分辨率。

Lecture 11 - Hardware Acceleration

CPU加速：以矩阵乘为例

  • 向量化
  • 并行
  • 寄存器分块（Register tiled）：矩阵分块，每个小块的数据都取到寄存器中，重用寄存器中的数据
  • 缓存分块

计算上很好解决，因为结构简单，并行和向量化很好写，访存上要尽量保证数据重用

image-20231127171928310

image-20231127172037687

image-20231127172252350

image-20231127172259739

Lecture - 12 GPU Acceleration

cuda语法，以矩阵乘为例

  • shared memory
  • cooperative fetching

Lecture 13 - Hardware Acceleration Implemention

needle

hw1

自动微分

关于代码结构

image-20231120170613255

在Python中，一个目录如果包含一个__init__.py文件，那么这个目录就被视为一个包（package）。这个__init__.py文件的作用是初始化包，可以在其中导入包需要的模块，或者定义需要的变量和函数。

在你给出的代码中，__init__.py文件导入了autograd模块中的Tensor、cpu和all_devices，以及ops模块中的所有内容。这样，当你导入needle包时，这些模块和变量就可以直接使用，无需再次导入。

至于autograd.py中为什么可以直接import needle，这是因为Python的导入机制允许一个模块导入其所在包的其他模块。当你在autograd.py中写import needle时，Python会查找needle包（也就是autograd.py所在的目录），并导入其__init__.py文件中定义的所有内容。

LAZY_MODE：不会立即计算cached_data，而是当需要的时候再计算

detach() 分离节点，使其只保留值，不保留庞大 inputs

算子梯度计算

正向传播要注意

  • 矩阵乘要用matmul而不是dot
  • tranpose看要求，对两个维度进行转换，用swapaxes，transpose是接受指定维度顺序的元组，改变整个张量的维度顺序

反向传播要注意：实现反向传播不应该再使用numpy的算子了，而是ops定义的算子，这样就可以通过计算图再计算梯度的梯度

  • 为什么求transpose梯度时要用transpose
  • reshape没有改变张量的数据，只是改变了布局，因此只要将形状回到改变前即可

拓扑排序

  • BFS：也叫Kahn算法，正向思维，找入度为0的点，删掉该点和相连的边，更新入度，重复过程直至所有点都被删除，如果有点剩余，则有环
  • DFS：深度优先，逆向思维，最先被放入栈中的节点是在拓扑排序中最后面的节点。确保了有向边的起始点比结束点先访问

reverse mode differentiation

按照伪代码来即可，注意要用框架中给的sum_node_list gradient_as_tuple,还要考虑op为None的情况

nn_epoch

三个错误

  • np.zeros()，要指定形状的话，形状外面要套括号 np.zeros((y.shape[0],W2.shape[1]))
  • relu肯定要用maximum返回Tensor，不然用max就返回一个整数了
  • relu的梯度计算，对输入node计算relu的结果判断是否大于零，大于零返回out_grad，否则返回0

hw2(网络模块，损失函数，优化器，dataloader，初始化)

初始化

uniform 表示均匀分布 normal 表示正态（高斯）分布

NN

主要要用参数类包装模块的参数

出现bug，排查后发现两处错误：

autograd.py正确
ops_logarithmic正确
ops_mathematic：
sofmax部分
layernorm部分
batchnorm部分

nn_basic：softmax是错误的，发现是axis传错了，传了多值元组，应该只有一个值

现在就是ops_mathematic的问题了

逆天 power_scalar的梯度计算写错了，为啥hw0没检查出来。。。。。

实现了Linear Flatten ReLU Sequential Residual几中网络模块

SoftmaxLoss损失函数

BatchNorm1d LayerNorm1d 归一化模块

Dropout正则化模块

Optimizer

实现了SGD和ADAM带weight_decay进行正则化

DATA

利用索引翻转数据

1
2
3
img = img[:, ::-1, :]#水平翻转
img = img[::-1, :, :]#上下翻转
img = img[:, :, ::-1]#颜色通道翻转

关于crop

这段代码实现了对图像进行零填充（zero padding）和随机裁剪（random crop）的操作。下面解释这个操作的具体步骤：

  1. 输入参数 img 是一个形状为 H x W x C 的图像数组，其中 H 表示图像的高度，W 表示图像的宽度，C 表示图像的通道数。
  2. 首先，我们对图像进行零填充。使用 np.pad() 函数，将图像的所有边缘（上、下、左、右）都填充为零。填充的大小由参数 pad_size 指定。填充后的图像数组形状为 (H+2pad_size) x (W+2pad_size) x C。
  3. 接下来，我们随机生成裁剪位置。我们使用 np.random.randint() 函数生成在范围 [0, max_shift] 内的随机整数，其中 max_shift 的值为 2*pad_size。这样可以确保裁剪位置在填充区域内，不会超出填充后的图像范围。
  4. 最后，我们根据随机生成的裁剪位置对填充后的图像进行裁剪，以恢复到原始图像的大小。我们使用裁剪位置和原始图像的高度、宽度来选择图像的子区域。裁剪后的图像数组形状为 H x W x C。
  5. 最终，函数返回裁剪后的图像数组。

通过这个操作，我们可以实现对图像进行零填充，然后在随机位置进行裁剪，从而生成与原始图像大小相同的裁剪图像。这在

Q5实战

为什么nn.Linear(dim,hidden_dim)只能有一个？？？

因为weight和bias使用numpy rand生成，rand生成以后seed会变化，所以结果不一样就过不了check

真正训练不会影响结果，但是test程序只是简单比较固定数值，导致了这个问题

写epoch的时候犯了错，直接用numpy的方法操作Tensor对象了，应该操作Tensor对象的cached_data属性或者numpy()

HW3（NDArray后端）

相关的文件

python类定义：ndarray.py

三个后端：

  • ndarray_backend_numpy.py
  • ndarray_backend_numpy_cpu.cc(编译成so调用)
  • ndarray_backend_numpy_cuda.cu(编译成so调用)

NDArray的重要属性，只记载类似元数据，具体的数据在device中，handle是python中管理地址的属性

strides表示在遍历多维数组时，从一个元素移动到下一个元素需要跳过的数据量。可以在不改变数据的情况下，改变strides改变数据格式
广播可以通过添加strides最后一维为0实现

1
A[i, j] => Adata[i * A.strides[0] + j * A.strides[1]]

offset表示数据偏移量，也是可以针对同样的数据获取不同的结果

1
2
3
4
5
6
def _init(self, other):
    self._shape = other._shape
    self._strides = other._strides
    self._offset = other._offset
    self._device = other._device
    self._handle = other._handle

重要函数：

构造函数：初始化上面的属性，包括从NDArray中构造，从numpy中构造，从其他构造。构造函数都是从其他来源构造NDArray

如果没有其他来源，可以用make创建

bug记录

用conda的base环境Python 3.8.3始终有循环导入的问题，经过长时间测试，发现ipynb中不会有这个问题，尝试更换了cmake版本和python版本后，终于在python的Python 3.10.12版本解决了这个问题。令人抓狂！

Python array operations

不修改数组在内存中的内容，而是修改shape和stride参数
关键在于搞清stride和shape的关系，计算stride的函数已经给出compact_strides，原理就是最前面的是第n维stride是后n-1维shape相乘，最后一维stride是1

permute相当于多维转置，除了shpe要转，sride也要转，这样可以在不改变内存的前提下实现转置